拓扑优化软件选择?
Optistruct拓扑优化,ANSYS Topology Optimization拓扑优化和COMSOL Optimization Module拓扑优化技术在轻量化设计中的各自的优势?考虑流体散热和结构受力分析中的优化问题,那款软件更适合?
同问,求回答。我只用过comsol的拓扑优化,感觉不是特别好,不知道是不是自己水平不够的原因
题主说的两个我都用过,comsol和ansys的比较,我更习惯用ansys的,但我是刚入门,ansys的模型拓扑优化之后还能修改细节,我觉得操作起来更方便。
谢亿民院士领导的中国团队——谢亿民科技,根据他提出的双向渐进结构优化法(BESO),研发了基于该算法的拓扑优化设计软件Ameba。用户可根据设计需要,对初始设计区域施加力学等边界条件,通过软件计算进行优化,求解时设计区域会像变形虫那样进化成各种形状,最终获得传力合理且仿生的形态。
3D打印中,多数拓扑优化是为了抑制残余应力、变形和过热,很少有将这些方法与悬垂角约束相结合。大阪工业科学技术研究所提出一种用于3D打印高精度自支撑形状的拓扑优化,不仅减少了3D打印时间和成本,而且还防止了由于变形导致的打印失败。
基于水平集的拓扑优化
固定设计域D由材料域Ω和空隙域D\\Ω组成,它们通过特征函数来区分。本研究采用基于水平集的拓扑优化,使用反应扩散方程。在该方法中,结构边界?Ω由水平集函数的等值面表示。此外,材料域Ω和空隙域D\\Ω通过水平集函数的符号来区分,如下所示:

特征函数用水平集函数表示φ如下:

最佳物料分配χφ,即水平集函数的分布φ, 通过求解时间演化方程确定如下:

其中t是虚拟时间,K是正参数,J’是目标优化问题的拓扑导数,并且r>0是正则化参数。扩散项不仅确保了水平集函数的平滑性φ,而且通过调整正则化参数来控制最优配置的几何复杂性r。我们设置了K=0.7和r=5.0X10-4。
自支撑约束
在这项研究中,引入亥姆霍兹型偏微分方程 (PDE),利用投影特征函数的梯度来限制悬垂角χφ。物理变量ψ∈H1(D)及其控制方程定义如下:
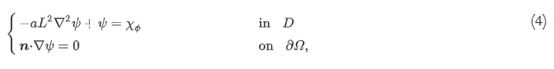
其中,a∈R+是各向同性扩散系数,L代表长度,n是向外法向量。扩散系数a影响过渡宽度ψ。换句话说,可以通过调节扩散系数来控制悬垂区域。此外,它还可以控制向下凸起的形状。
图 1显示了增材制造中悬垂区域的示例。需要支撑结构来构建与水平面成一定角度以上的悬垂区域。在显式悬垂角约束中,检测悬垂区域的常用方法是评估法向量之间的角度n从结构边界?Ω和构建方向。在这项研究中,通过直接评估法向量的内积来检测悬垂区域nψψ从结构边界?Ω和阈值角度向量d1和d2。对于 2D 问题,阈值角度向量d1和d2为

当两个内积都取正值时,就会检测到悬垂区域。因此,约束悬垂角的条件为

其中R(s)?(s+|s|)/2个表示斜坡函数。此外,悬垂角约束将上述方程归一化并定义为

为了验证公式化的PDE和悬挑角约束,提供了使用FEM的数值示例,如图2所示。分析域D由两个域组成,图1所示的目标模型为材料域Ω,另一个区域为空隙域D\\Ω。
D域的尺寸为1.0X1.2,并被离散为二阶三角形单元的网格。扩散系数a设置为1,代表长度L设置为1.0,阈值角度θ0设置为45。图2(a)显示了通过求解方程(4)获得的分布ψ。ψ从材料域平滑过渡到空隙域。图2(b)、(c)和(d)表明,内积均为正值的区域为外伸区域。
图2(e)显示了从余弦值与法向量和建筑方向d的内积的比较中获得的悬垂区域nψ。
与上述传统方法相比,所提出的约束函数能够检测阈值角附近的悬挑区域。这意味着在优化过程中,阈值角附近的悬伸区域也被优化以满足约束。图2(f)显示了扩散系数a设置为1X10-3时的结果。该结果表明,扩散系数影响悬垂区域的评估面积。3D问题中的悬垂角约束通过添加正交平面的阈值角向量来给出,如下所示:

其中
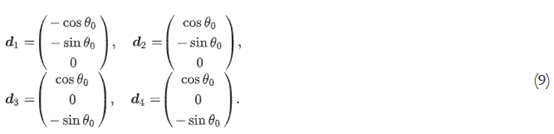
图 3显示了使用等式 1/4 半球模型对悬垂区域进行评估的结果。在 3D 和 2D 情况下都可以检测到悬垂区域。接下来,使用伴随变量法导出悬垂角约束的拓扑导数。伴随变量ψ?∈H1(D)及其伴随方程定义如下:
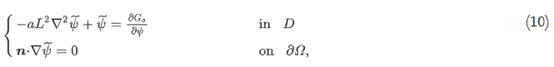
其中
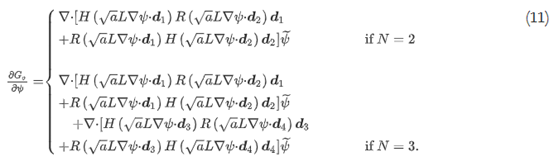
H(s)?dR(s)/ds是 Heaviside 函数,并且N是空间维度的数量。作为方程式中的唯一源项。受特征函数的影响χφ,悬垂角约束的拓扑导数 Go推导如下:

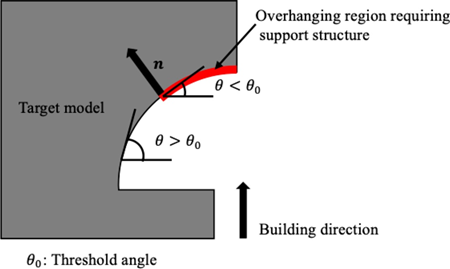
图 1 增材制造中悬垂区域的示意图。
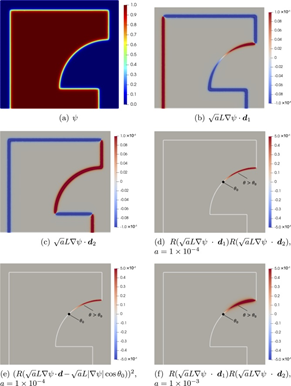
图 2 悬垂角约束的数值示例。
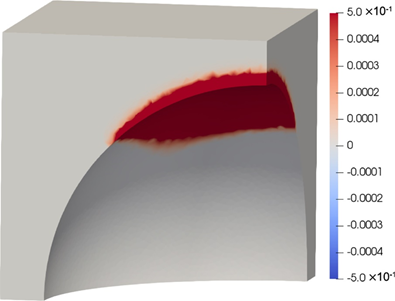
图 3 3D 模型的数值示例。
滴水效应的热模型
如介绍中所述,上述悬垂角约束会产生向下凸起的形状,这种现象称为滴水效应 。在实际制造中,这些形状会阻碍热流,导致过热,从而产生不良缺陷,例如孔隙率和表面质量下降。因此,研究者提出了一种通过考虑增材制造过程中的散热来抑制滴落效应的方法。以往提出的模型,热通量仅应用于悬垂边界,而不是逐层应用。在本研究中,考虑将热通量应用于每一层悬垂边界的热模型。首先,为了表示构建过程,域Ω分为m在建筑方向上具有固定厚度的层。域Ω由每个域定义Ωi,1≤i≤m。 此外,域Ω由三个子域组成:激活域ΩA, 无效域ΩI, 和激活域Ωq。 激活域ΩA被具有导热性的各向同性材料占据k, 并且固定温度边界条件应用于基板ΓT。 那么,温度场Ti∈H1(ΩA)有热通量q应用于悬垂边界Γq添加层的Ωq由以下控制方程表示:

指数i=1,2……m,其中Tamb是散热器的基板的温度。
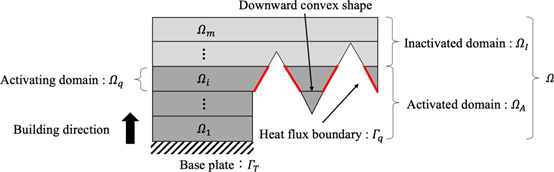
图 4 建筑过程中热模型的域和边界。
提高各域散热的热约束功能Ωi定义如下:

接下来,使用伴随变量方法导出热约束的拓扑导数。伴随变量T—∈H1(ΩA)及其伴随方程定义如下:
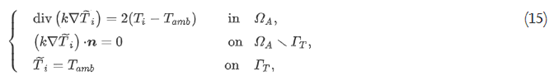
随后,热约束的拓扑导数Gt推导如下

失真约束
预测局部残余应力和变形的力学模型采用固有应变法,对每一层施加应变,如图5所示。域分为具有固定厚度的层n,如在热模型中,由三个子域组成。域Ω由每个域定义Ωj,1≤j≤n。
每个子域区域Ωj由激活状态决定, 激活域ΩA由各向同性弹性材料占据,并在基板上施加固定位移边界条件Γu。 位移uj∈H1个(ΩA)N具有固有应变?inH应用于域Ωinh由以下控制方程表示:
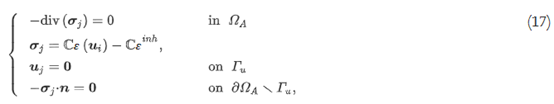
对于所有指数j=1个,2个,……,n,其中σ表示柯西应力张量,C表示弹性张量,和?(u)表示由定义的总应变张量ε(u)?1/2(?u+(?u)? ). 请注意,上式表示不考虑塑性变形的弹性分析。固有应变?inh在域Ωinh中定义如下:

其中X表示位于ΩA。 在本研究中,3D情况下固有应变分量设为εxinh=εyinh=?0.0025和εxinh=0。此外,为了计算成本,在建筑方向上以每层 1 毫米划分域。详细讨论识别固有应变?inh的方法,使用 FEM 的构建过程算法,以及层数n适用于拓扑优化。建造过程结束后的残余应力和变形表示如下:

失真约束函数使用P范数函数定义,如下:

其中b≥2是本研究中设置为5的惩罚参数。接下来,使用伴随变量法导出失真约束的拓扑导数。伴随变量u—j∈H1(ΩA)N及其伴随方程定义如下:
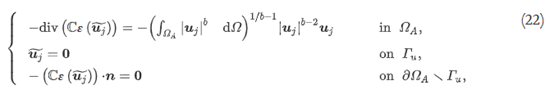
指数j=1,2,……n和失真约束的拓扑导数Gu推导如下
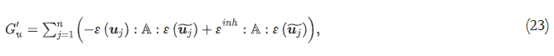
其中常数四阶张量A由下式给出
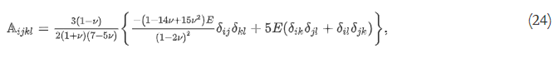
其中E,ν,δ分别是杨氏模量、泊松比和克罗内克。
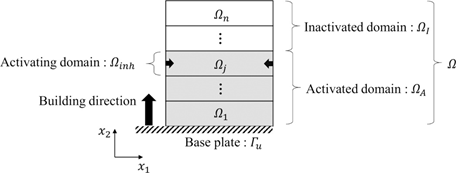
图 5 建筑过程中机械模型的领域和边界。
优化问题的表述
首先,我们将上述约束纳入最小均值合规性问题。在这个问题中,材料域Ω固定在边界Γv, 和牵引力t应用于边界Γt。位移场表示为v∈H1(Ω)N在静态平衡状态下,目标函数定义为

通过在目标函数中包含约束函数作为惩罚项,将优化问题表述为无约束问题,如下所示:
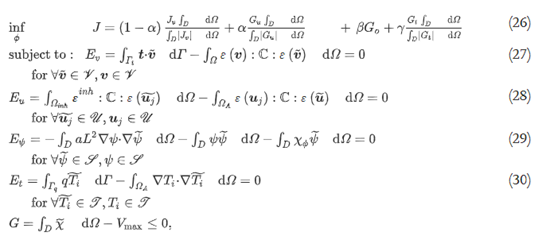
指数i=1,2……m, j=1,2,……n, 0≤α≤1,β和γ是加权参数。在上面的公式中,G表示体积约束,并且Vmax是材料D的体积上限, 此外,功能空间定义如下:
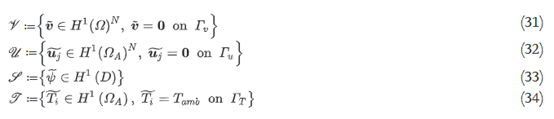
最小均值合规性问题称为自伴随问题。因此,伴随变量相当于位移场v, 最小均值合规性问题的拓扑导数推导如下:

接下来,考虑内部发热的稳态热传导问题。在这个问题中,热源Q应用于设计域D和温度P=Pamb固定在边界Γp。 温度场表示为p∈H1 (Ω)在静态平衡状态下,目标函数定义为

这个目标函数称为热依从性 。随后,通过替换方程(26)中的目标函数和方程(27)中的控制方程,优化问题公式如下:
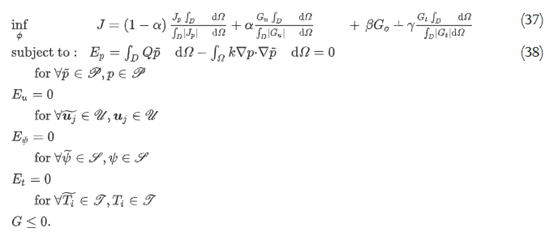
功能空间P定义如下:

这个优化问题也是一个自伴随问题,类似于最小均值合规问题。因此,该优化问题的拓扑导数推导如下:

优化算法如下:
水平集函数初值φ设置为固定设计域D。
通过FEM求解方程(4)、(13)和(17)中定义的目标物理和每个状态变量的控制方程。
计算目标物理的目标函数J。
如果目标函数收敛,则优化过程终止;否则,通过FEM求解方程(10)、(15)和(22)中定义的每个伴随变量,并计算拓扑导数的和J’。
使用等式(3)给出的时间演化方程更新水平集函数;然后,优化过程返回到第二步骤。
该优化算法使用开源PDE求解器FreeFEM++[48]实现。
在本研究中,从计算成本的角度使用ersatz 材料方法 区分材料域和空域。具体来说,我们假设空域具有较小的材料特性,并且材料域和空域之间的边界具有平滑分布的材料特性。随后,扩展的弹性张量C和导热系数k?用于求解固定设计域D中的控制方程定义如下:

其中,Hφ(φ;w)定义为

这里,w表示过渡的宽度,并且C是材料域和空隙域的材料属性之比。此外,方程(4)、(10)通过用以下Heaviside函数代替特征函数来求解:

设置C=1.0×10-3,w=0.5,ξ=0.9。
接下来,介绍方程(30)中定义的热传导方程的近似解方法。这里使用Dirac delta函数将边界积分替换为域积分δ(x),,如下所示:

三角函数δ(x)使用 Heaviside 函数表示Hψ(ψ;w), 如下:

其中nψ表示法向量Hψ(ψ;w). 上式可以改写为

然后,使用法向量的内积仅提取悬垂边界nψ和建筑方向d, 如下:
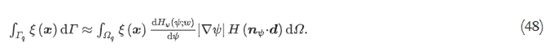
将上述方程代入方程(30),得到
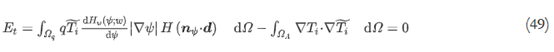
因为斜坡函数的导数不能定义为s=0, 一个小参数?s∈R+被引入并且该函数被定义为近似斜坡函数R?,如下:

实施中,设置?s=1×10?4。
悬垂角约束参数的影响
本小节给出了仅具有外加悬挑角约束的优化示例。优化示例考虑了对称2D MBB光束的最小平均柔量问题,如图6所示

图 6。MBB 光束的设置,尺寸以毫米为单位。
本研究采用的材料为AlSi10Mg,其杨氏模量为75GPa,泊松比为0.34。允许体积的上限设置为固定设计域的50%。公式(4)中的代表长度设置为L=25mm。阈值角度设置为为θ0=45°。在这里,我们检查了方程(4)中与悬垂角约束β和扩散系数α相关的参数的影响。图7、图8显示了在不同悬垂角约束和扩散系数下获得的一组优化结果。如图7所示,增加β消除了悬垂区域,但产生了许多向下凸起的形状。相反,增加扩散系数α会抑制滴水效应,但会产生悬垂区域,如图8所示。这是因为扩散系数影响悬垂区域的评估面积,如图2所示。换句话说,如果α设置得大于5X10-3,则评估区域太大。因此,扩散系数α应设置在1X10-4至1X10-3的范围内。在以下优化示例中,设置了β=20和α=5X10-4。该结果表明,仅约束悬垂角度是不够的。因此,为了满足自支撑约束,有必要将角度约束与其他约束相结合,比如所提出的热约束。
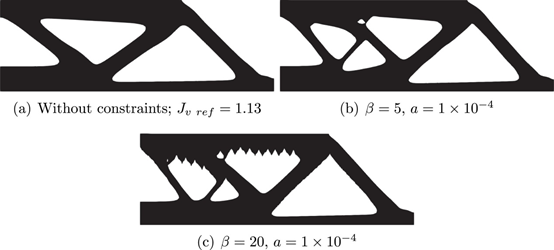
图 7 不同悬垂角约束参数下的优化MBB梁
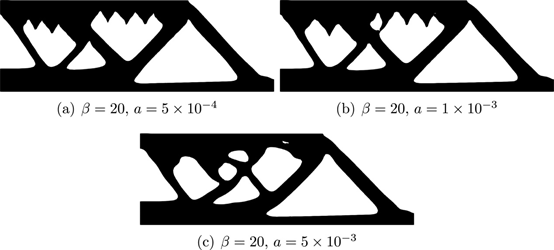
图 8 不同扩散系数下优化的 MBB梁
热约束参数的影响
本小节介绍了优化示例,其中在悬垂角度约束中添加了热约束以抑制滴落效应。与等式(13)相关的每个参数设置如下。导热材料的热导率为119W/mK。所施加的热通量q设置为10W,基板温度设置为Tamb=0°C。在这里,我们检查了与热约束相关的参数的影响γ和层数m在固定的设计领域。下图 9显示了在不同热约束下获得的优化结果γ,其中固定设计域分为m=50层。可以看出,通过设置γ大于 0.2,滴水效应被完全抑制。此外,作为γ增加,每个成员变得更厚,这有望改善散热。然而,设置γ在0.2 和 0.4 之间是合适的,随着增加γ超过 0.4 会降低依从性Jv超过 10%。图 10显示了不同层数下得到的优化结果m,其中γ设置为 0.2。图中的白线表示层边界。当层数小于10时,滴水效果不再被抑制。 该结果表明,如果将层数设置为可以分割向下凸起形状的大小,则可以通过考虑热约束来抑制滴水效应。在以下优化示例中,γ=0.2.

图 9不同热约束参数下优化的 MBB 梁
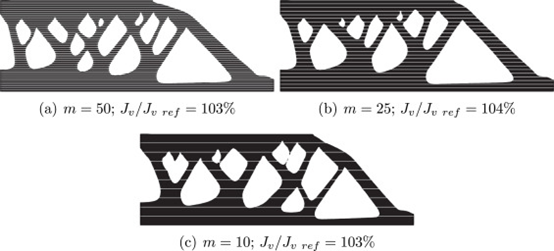
图 10不同层数下的优化的 MBB 梁
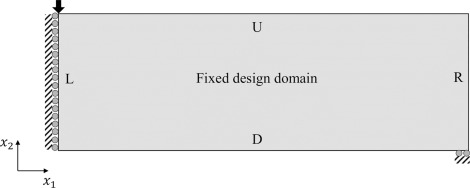
图 11 MBB 梁构建方向的设置
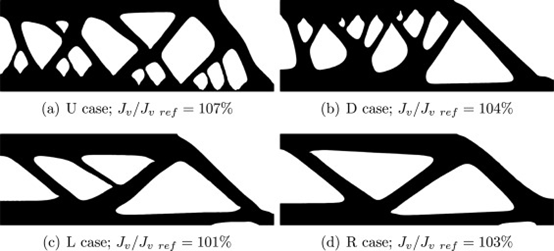
图 12 不同建筑方向下优化的 MBB 梁
建筑方向的影响
在这里,针对不同建筑方向的优化示例被提出来证明所提出的自支撑约束的有效性。如图11所示,建筑方向考虑四种情况,固定设计域的U、D、L、R各边作为底板。固定设计域中的层数对于 U 和 D 设置为 25,对于 L 和 R 设置为 50 层。图 12显示了在不同建筑方向下获得的优化结果。所有最佳形状都抑制了滴水效应并满足任何建筑方向的悬垂角度约束。特别是,L 的形状实现了与无约束形状等效的顺从性。因此,选择合适的建筑方向将在不影响结构性能的情况下产生可打印的设计。
悬垂角的影响
本小节给出了针对不同阈值角度的优化示例,以进一步证明所提出方法的有效性。在这里阈值角的分别设置为θ0=30°,45°,60°。示例包括图13中所示的 2D MBB 和悬臂梁。每个参数设置为与MBB 光束相同的值。图14、图15为不同阈值角度下的优化结果。在 MBB 示例中,获得的形状没有创建低于指定阈值角度的成员。然而,在悬臂示例中,有一些违反了图 15中的约束。 这是因为约束函数被视为惩罚项,这意味着使用相同的惩罚参数增加阈值角度可能无法完全满足约束。因此,应该修改惩罚参数。此外,即使阈值角度为θ0=60°。 这些结果证明了所提出的自支撑约束方法的有效性。
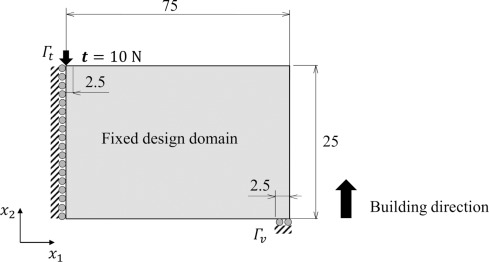
图 13悬臂梁的设置,尺寸单位为毫米。
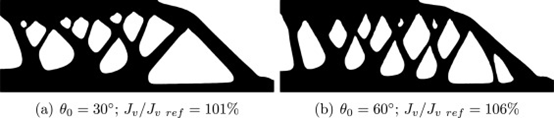
图 14 在不同阈值角度下优化的 MBB梁
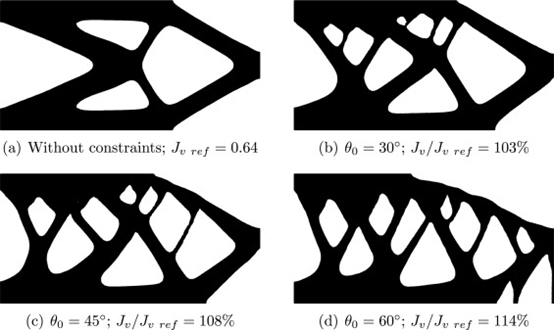
图 15不同阈值角度下的优化悬臂梁
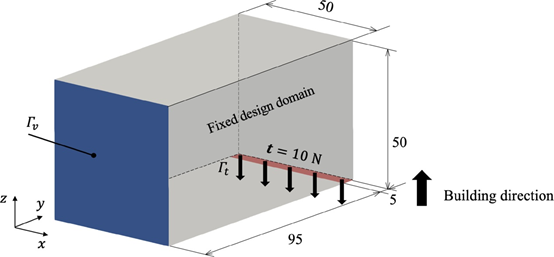
图 16 3D 悬臂梁的问题设置,尺寸以毫米为单位。蓝色面表示完全受压状态,红色面表示施加牵引力,建筑方向为正z-轴。
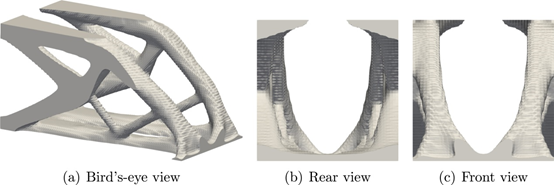
图 17 优化的3D悬臂梁无约束;Jv ref=0.031

图 18 优化的具有自支撑约束的3D悬臂梁;Jv/Jv ref=110%.
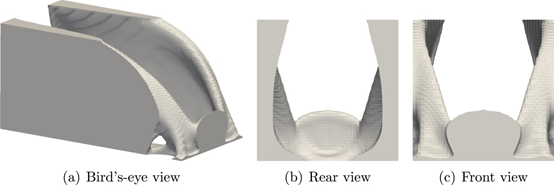
图 19 优化的具有自支撑和畸变约束的3D悬臂梁;Jv/Jv ref=114%
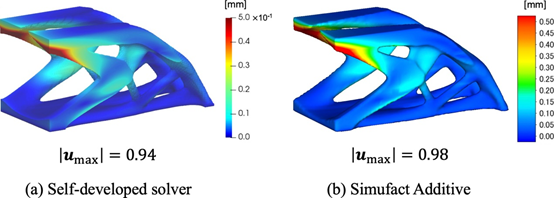
图 20 自研求解器与Simufact Additive得到的畸变对比。
结合失真约束
首先,我们考虑3D悬臂梁的最小平均柔度问题。固定设计域和边界条件如图16所示。允许体积的上限设置为固定设计域的20%。公式(4)中的代表长度设置为L=50mm。阈值悬垂角设置为θ0=45°。固定设计域在建筑方向上分为热约束层m=25和变形约束层n=50。与等式(26)中的失真约束相关的加权参数被设置为α=0.05。其他参数是在前面的优化示例中设置的参数。图17、图18和图19分别显示了在无约束、有自支撑约束以及有自支撑和变形约束的情况下获得的优化结果。两种约束施加的形状都会抑制滴落效果,并满足悬挑角度约束。此外,比较每个形状的顺应性,可以观察到变形约束对结构性能的影响是最小的。图 20显示了使用自主开发的固有应变方法和 Simufact Additive(Simufact Engineering Gmbh,德国汉堡)获得的变形的比较。显然,失真分布结果显示出可接受的一致性水平。图21显示了使用所提出的热模型和瞬态热分析 (Simufact Additive) 获得的每层峰值温度的比较。注意,图21(a)中的温度场是从方程(13)的无量纲版本获得的。在同一区域出现过热表明所提出的热模型检测到过热。所提出的热模型在计算上比瞬态热分析便宜;然而,如果堆积了更多的层,则建筑方向上的温度梯度减小,并且可能无法准确评估过热。因此,通过与瞬态热分析获得的优化结果进行比较来进行验证仍然是未来研究的主题。以下讨论基于Simufact Additive获得的数值结果。图22和图23显示了每个最佳形状的变形和峰值温度的比较。没有约束的最佳形状在悬垂区域具有较大的变形和过热。相比之下,所提出的自支撑约束不仅抑制了低于阈值角度的构件的产生,而且还减少了变形和过热。变形和过热的减少与悬垂区域的减少和散热的改善相关。此外,通过添加失真约束,失真的最大值|Umax|减小,失真分布变得均匀。然而,包括构建过程在内的约束增加了计算成本,因为必须为每个层计算这些约束。因此,在实际设计中,根据需要添加失真约束的过程比考虑所有约束更为现实。
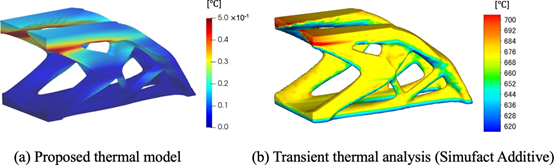
图 21 所提出的热模型和瞬态热分析 (Simufact Additive) 的峰值温度比较。
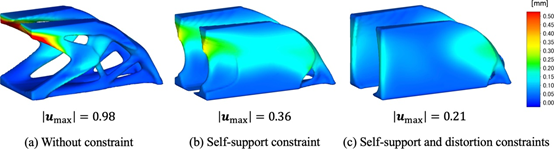
图 22优化的 3D 悬臂梁的构建过程引起的变形比较。
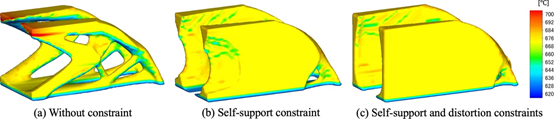
图 23 优化的 3D 悬臂梁的峰值温度比较。
接下来,考虑 3D 热传导模型的热扩散率问题。在等式(38)、(39)中固定的设计域和边界条件如图24所施加的热源Q设置为 10 W,温度设置为Pamb=0℃。允许体积的上限设置为固定设计域的 15%。方程式(4)中的代表性长度L=50mm。阈值悬垂角设置为θ0=45°。 固定设计域在建筑方向上分为m=25热约束层和n=50失真约束层。图25、26、27分别显示了在无约束、有自支撑约束以及有自支撑和失真约束的情况下获得的优化结果。每个约束对热顺应性的影响类似于悬臂梁的结果。图 28、图 29显示最佳形状的变形和过热的数值结果。与悬臂梁类似,施加自支撑约束的形状没有违反悬垂角度约束的构件,从而减少了变形和过热。对于失真约束也是如此。在 3D 数值示例中,设置了通过 2D 验证确定的自支撑约束的每个参数。因此,每个参数都独立于问题设置。这些示例表明,所提出的方法可以生成可以使用 AM 高精度制造的自支撑形状。这不仅减少了制造时间和成本,而且还防止了由于变形导致的制造失败。这意味着可制造性不需要设计更改
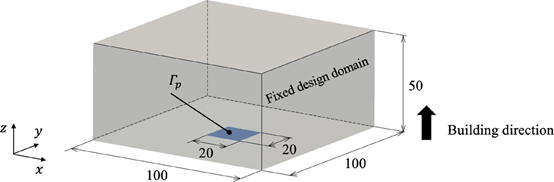
图 24。以毫米为单位的尺寸的 3D 热传导模型的问题设置。蓝色面为散热片,建筑方向为正z-轴。

图 25。优化的3D热传导不受约束;Jp ref=170495
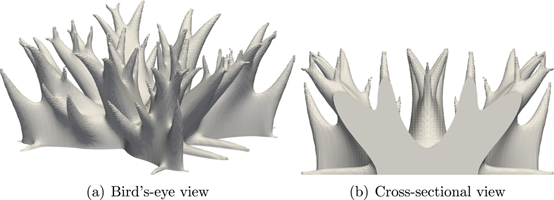
图 26。具有自支撑约束的优化 3D 热传导;Jp/Jp ref=109%
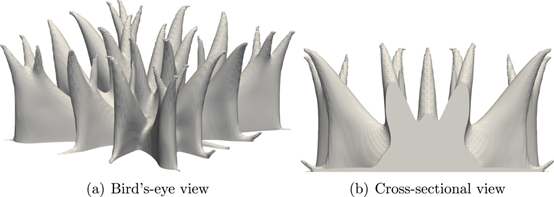
图 27。具有自支撑和变形约束的优化 3D 热传导;Jp/Jp ref=112%
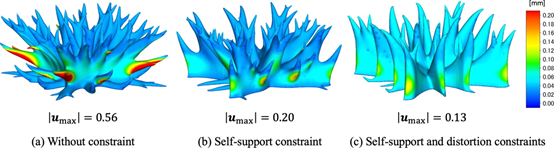
图 28。优化的 3D 热传导模型的构建过程引起的变形比较。
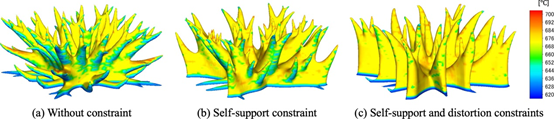
图 29。优化的 3D 热传导模型的峰值温度比较。
本研究的主要贡献总结如下。
1.提出了一种具有可调滴水效应程度的亥姆霍兹型 PDE,并使用角度向量制定了悬垂角约束,并通过数值示例进行了验证。二维优化实例表明,单独调整惩罚参数β和扩散系数α不能产生自支撑形状。
2.提出了建筑过程的热模型,并制定了使每层散热最大化的热约束。二维优化示例表明,所提出的热约束抑制了滴落效应。还研究了约束参数对滴水效果和结构性能的影响。通过三维数值示例证明了所提出的热模型评估过热的能力。
3.提出了一种基于建筑过程中固有应变法的力学模型,并制定了抑制变形的约束条件。
4.通过在目标函数中包含约束函数作为惩罚项来制定无约束优化问题,并使用 FEM 构建优化算法。通过优化实例演示了调整每个惩罚参数的方法。
5.二维优化实例表明所提出的自支撑约束的有效性,设计变更对结构性能的影响很小。
6.三维优化示例表明,所提出的自支撑约束会产生具有抑制变形和过热的自支撑形状。此外,失真约束的添加导致更均匀的失真分布。所提出的方法可以通过增材制造实现无支撑和高精度制造。




