轨迹优化06. 镇定、跟踪 & 调节
从本篇开始,连续3篇开始介绍跟性能指标(目标函数)有关的轨迹优化问题
先上图:

解释一下三个概念:
(1)镇定:状态x(t)渐近稳定,也就是当t->∞时,x(t)->0
(2)跟踪:状态x(t)的跟踪误差e(t)=z(t)-x(t)或输出y(t)的跟踪误差e(t)=z(t)-y(t)镇定
(3)调节(Regulation):说到英语,其实在机器学习里这个英语单词被翻译为 正则化,而正则化的目的是为了 “避免过拟合”,通常有L1,L2等方法,其实在最优化里面,调节通常用的是输入的L2

这段主要是参考 西北工业大学 郭建国老师的 《现代控制理论》课程,详见可以看MOOC
我们这边还是先考虑最简单的线性系统
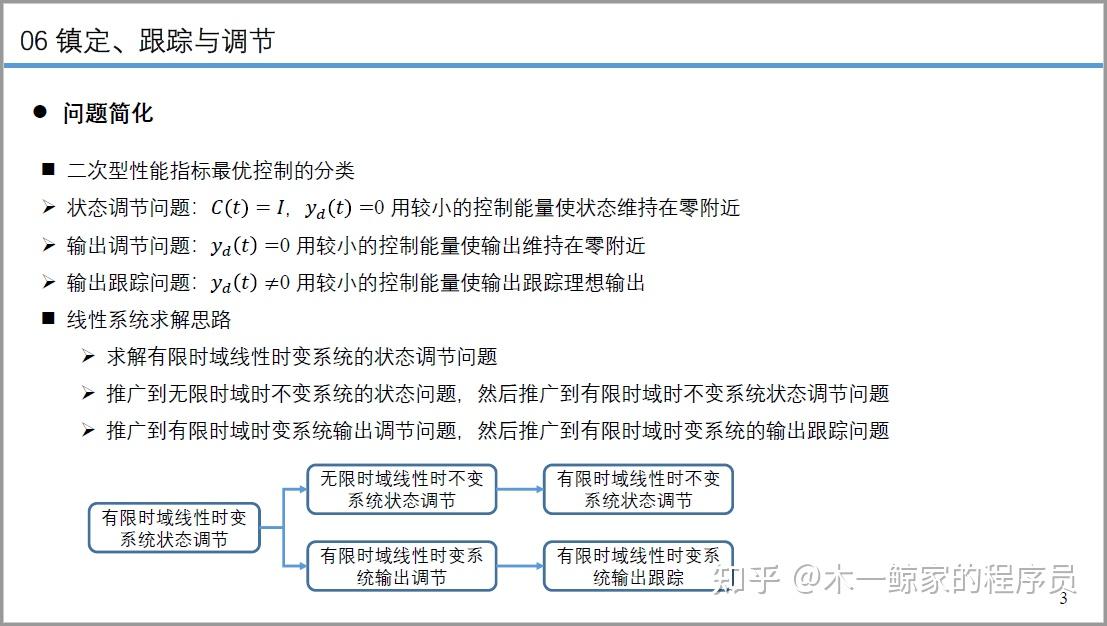
状态调节问题:其实就是 状态镇定 + 调节
输出调节问题:其实就是 输出镇定 + 调节
输出跟踪问题:其实就是 输出跟踪 + 调节
以下主要讨论 线性系统的二次型性能指标的轨迹优化问题
即:系统的动力学是线性系统,轨迹优化的目标函数是二次型性能指标的问题

目标函数的终端指标是二次型,积分指标也是二次型

采用最优控制里面的最大值原理,按照其步骤写出来:
(1)哈密顿函数
(2)正则方程
(3)控制方程
(4)横截条件
根据横截条件,我们可以做一个假设,哈密顿算子与状态满足线性关系,于是:

可以得到一个结论: 矩阵Riccati微分方程,这个方程在最优化问题(最优控制,轨迹优化,最优估计)都扮演着重要的角色
求得Riccati微分方程的解(具体解法可以参考《运动感知》专栏中 《状态估计03. Riccati方程》),进而可以得到最优控制解,于是可以设计出 状态反馈,也就是实现了闭环最优控制,也就是实现了轨迹优化的闭环

考虑无限时域,或者换句话来说,稳态性能,于是不需要考虑终端条件,只需要考虑积分条件
这里可以考虑Raccati微分方程,给定终端时刻,逆时间求解出矩阵P(t),一个重要的结论是:矩阵P(t)在远离终端时趋近于一个常数矩阵
***系统能控

矩阵P(t)在远离终端时趋近于一个常数矩阵,于是P(t)的导数也为0,而经典的Raccati微分方程变成了Raccati代数方程
4. 有限时域线性时变系统输出调节

与状态调节问题相比,唯一区别在于权值系数矩阵发生了改变
***系统能观测

进一步推广到无限时域线性定常系统的输出调节问题,要求系统能控能观测。

而输出跟踪问题,只是将输出项变成输出跟踪误差项,求解过程的极大值原理相似

只不过此时,线性关系已经不是传统意义的比例项,而是比例项 + 偏置项的一次关系
Raccati微分方程没变,只是多了一个补充微分方程,以及补充边界条件

除状态和输入项,其他的时变系数均变为常系数

1-7都可以总结为上图的问题
而1-7只是下图的简化

这一篇还存在两个坑:
(1) 矩阵Raccati微分(代数)方程如何求解?
(2) 非线性动力学系统如何求解?
且听以后填坑~~~
Reference
- 西北工业大学 郭建国 《现代控制理论》




